Teorema del coseno
La geometría es una ciencia y una parte del área de las matemáticas que se encarga de estudiar las diferentes propiedades y las medidas que tienen todas las figuras que están en el plano y en el espacio. Existen dentro de esta área de estudio muchas figuras geométricas, ángulos, superficies y teoremas, como por ejemplo el teorema del coseno. Este teorema lo podemos estudiar y encontrar más específicamente dentro del área de la geometría euclidiana y es un teorema en el cual los triángulos indican las longitudes de sus lados y sus relaciones con los lados restantes que los conforman.
¿Qué es el teorema del coseno?
Es una generalización del teorema de Pitágoras en el cual si aplicamos el teorema en un triángulo rectángulo nos brinda una relación de la longitud de un lado con las longitudes de los otros y con el coseno del ángulo formado por éstos.
Definición
El teorema del coseno es el teorema que nos indica que el cuadrado de la longitud que tiene un lado es la suma de los cuadrados de las longitudes que tienen los lados restantes restando el duplo del producto de las longitudes multiplicado por el coseno que tiene el ángulo que se encuentra opuesto al lado que se está estudiando.
Historia del teorema del coseno
La historia del teorema del coseno surge de los Elementos de Euclides, los cuales contenían una aproximación geométrica de la generalización del teorema de Pitágoras: el triángulo obtusángulo y el de un triángulo acutángulo. Tiempo después surgió la trigonometría árabe-musulmana de la Edad Media que evolucionó el teorema, el astrónomo y matemático al-Battani generalizó el resultado de Euclides en la geometría esférica a principios del siglo X, lo que permitió efectuar los cálculos de la distancia angular entre el Sol y la Tierra.
En este periodo también se establecieron las primeras tablas trigonométricas para las funciones seno y coseno lo que permitió a Ghiyath al-Kashi, poner el teorema bajo una forma utilizable para la triangulación durante el siglo XV.
Explicación
El teorema del coseno nos dice que el cuadrado que tiene la longitud de un lado es igual a la suma de los cuadrados que tienen las longitudes de los demás lados menos el duplo del producto de dichas longitudes multiplicado por el coseno del ángulo opuesto al lado en cuestión.
Fórmula
La ley o teorema de los cosenos por medio de su fórmula establece que:
c2 = a2 + b2 – 2·a·b·cos c
De hecho, esta formula es muy parecida al teorema de Pitágoras excepto que para el tercer término y si C es un ángulo recto el tercer término es igual 0 porque el coseno de 90° es 0. De esta forma, el teorema de Pitágoras es un caso especial de la ley de los cosenos.
La ley de los cosenos también puede establecerse como:
b2 = a2 + c2 – 2·a·c·cos b
a2 = b2 + c2 – 2·b·c·cos a
Aplicaciones del teorema del coseno
El teorema del coseno puede ser utilizado en triangulación para resolver un triángulo, y determinar:
- El tercer lado de un triángulo cuando conocemos un ángulo y los lados adyacente.
- Los ángulos de un triángulo cuando conocemos los tres lados.
Demostración
Por desglose de áreas cuando el ángulo es agudo: un cierto número de las demostraciones del teorema hacen intervenir un cálculo de áreas. Es importante remarcar que
- a2, b2, c2 son las áreas de los cuadrados de lados respectivos a, b, c.
- ab cos(γ) es el área de un paralelogramo de lados a y b que forman un ángulo de 90°-γ (para una prueba, ver el apéndice).
- Dado que cos(γ) cambia de signo dependiendo de si γ es mayor o menor a 90°, se hace necesario dividir la prueba en dos casos
Por el teorema de Pitágoras
Notemos que el teorema de cosenos es equivalente al teorema de Pitágoras cuando el ángulo es recto, por eso solo es necesario considerar los casos cuando c es adyacente a dos ángulos agudos y cuando c es adyacente a un ángulo agudo y un obtuso.
Importancia
El teorema del coseno tiene un papel de gran importancia dentro del área del cálculo y la definición de las superficies y volúmenes. De la mano con la teoría de la desigualdad triangular, el teorema de los cosenos y de las tangentes nos permiten poder realizar una caracterización de los elementos conformantes los cuales implican las longitudes de los lados y las amplitudes que tienen los ángulos que están en el interior de los triángulos para poder distinguirse entre los ángulos que conforman un triángulo.
Es importante también porque es considerado como una generalización del Teorema de Pitágoras que es aplicado únicamente a los triángulos rectángulos, mientras el teorema de los cosenos establece una caracterización sobre cualquier tipo de triángulos, incluyendo a los triángulos rectángulos, para los cuales, el coseno del ángulo opuesto a la hipotenusa es 0, regresando al histórico resultado.
Ejemplos del teorema del coseno
Algunos ejemplos que podemos citar con respecto al teorema del coseno son los siguientes:
Primer ejemplo resuelto
ϒ = 45°, b = 10, a = 15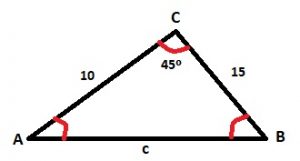
c2 = a2 + b2 – 2ab cos ϒ
c2 = 152 +102 – 2(15)(10) cos 45
c = 10.62
a2 = b2 + c2 – 2bc cos α
152 = 102 + 10.622 – 2(10)(10.62 cos α
152 – 102 – 10.622 = – 2(10)(10.62) cos α
(152 – 102 – 10.622 )/ – 2(10)(10.62) = cos α
α = 93.3°
b2 = a2 + c2 – 2ac cos β
102 = 152 + 10.622 – 2(15)(10.62) cos β
102 – 152 – 10.622 = – 2(15)(10.62) cos β
(102 – 152 – 10.622 )/ – 2(15)(10.62) = cos β
β = 41.7°
Segundo ejemplo
β = 73°50′, a = 87, c = 14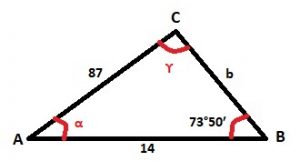
b2 = a2 + c2 – 2ac cos β
b2 = 872 + 142 – 2(87)(14) cos 73°50′
b = 84.18
c2 = a2 + b2 – 2ab cos ϒ
142 = 182 + 84.182 – 2(87)(84.18) cos ϒ
142 – 872 – 84.182 = – 2(87)(84.18) cos ϒ
(142 – 872 – 84.182 )/– 2(87)(84.18) = cos ϒ
ϒ = 9.2°
a2 = b2 + c2 – 2bc cos α
872 = 84.182 + 142 – 2(84.18)(14) cos α
872 – 84.182 – 142 =– 2(84.18)(14) cos α
(872 – 84.182 – 142 )/ – 2(84.18)(14) = cos α
α = 96.98°
¿Cómo citar este artículo?
Briceño V., Gabriela. (2018). Teorema del coseno. Recuperado el 24 febrero, 2024, de Euston96: https://www.euston96.com/teorema-del-coseno/