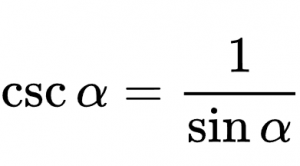Cosecante

La función cosecante es una antigua función en el área de la matemática. Fue mencionado en los trabajos de G. J. von Lauchen Rheticus en el año1596 y E. Gunter alrededor del año 1620. Fue ampliamente utilizado por L. Euler durante el año 1748 y T. Olivier, Wait y Jones en 1881. La definición clásica de la función cosecante para argumentos reales es: "la cosecante de un ángulo en un triángulo en ángulo recto es la relación que existe entre la longitud de la hipotenusa y la longitud del ángulo opuesto". Esta descripción es válida para cuando este triángulo no es degenerado. Esta aproximación se puede expandir a valores reales arbitrarios si se considera el punto arbitrario en el plano cartesiano y se define como la razón suponiendo que α es el valor del ángulo entre la dirección positiva del eje y la dirección desde el origen hasta el punto.

Temas relacionados

Coseno, cotangente, seno, teorema del coseno

¿Qué es la cosecante?

Se conoce como cosecante a la función inversa del seno de un arco o de un ángulo. Es un término muy utilizado en el área de la matemática cuando está relacionada con el área de la geometría.

Características de la cosecante

Las principales características de la cosecante son las siguientes:

• Se representa con las letras csc o cosec.
• Es una relación de trigonometría inversa al seno.
• Es conocida como el inverso multiplicativo.
• Su dominio es R – { k · π } con k ∈ Z
• El recorrido de la cosecante es R – ( – 1, 1 ).
• No corta el eje X ni tampoco lo hace con el eje Y.
• Una característica importante es que es impar lo que quiere decir que es simétrica con respecto al origen: cosec (- x) = – cosec (x).
• También tiene infinitos mínimos que son relativos en los puntos de la forma (  π/2 + 2·k·π, 1 ) – con k ∈ Z
• Es periódica de periodo 2π cosec ( x ) = cosec ( x + 2π ).
• También posee asíntotas verticales en los puntos de la forma x = k · π con k∈
• No se encuentra acotada.

Para qué sirve

Al igual que las demás funciones trigonométricas son útiles por ejemplo en el campo de astronomía ya que sirve para medir distancias entre las estrellas, en la medición de distancias entre puntos geográficos, y en sistemas de navegación por satélites. Son muy funcionales en el caso de la construcción de casas o edificios para conocer las medidas que se deben hacer. También es útil en la ingeniería civil, para calcular distancias, ángulos de inclinación o de peralte de una carretera. En el desarrollo científico se utiliza en la elaboración de métodos numéricos por parte de matemáticos para hacer ecuación diferencial o resolver una integral que no se pueda trabajar con los métodos convencionales.

Cómo se calcula

La fórmula para averiguar la cosecante es la siguiente:

Csc α = 1 / sin α = c / a

Derivada de la cosecante

La derivada de la cosecante de una función será la misma a menos la cosecante de la función por la cotangente de la función y también por la deriva de la función. La fórmula es la siguiente:

F (x) = cosec u

F´(x) = – ( u ㆍcosec u ) / ( sen² u ) = –u ㆍcosec u ㆍcotg u

Integral

La fórmula que se utiliza para la integral de la cosecante es la siguiente:

∫ csc u ㆍdu = – log (cot u + csc u)

Esta cosecante su puede averiguar cuando se dominan fórmulas de derivación

Dominio y rango

Importante es recordar que el dominio de una función está conformado por todos los valores de entrada que una función trigonométrica puede llevar a cabo. Los dominios de la cosecante se encuentran restringida y únicamente puede ser utilizada para las funciones de medir los ángulos con los números de salida. Cada vez entonces que el lado terminal que tiene un ángulo esté a lo largo del X-eje (donde y es igual a 0), no se podrá ejecutar la función cosecante del ángulo.

Función inversa

En el área de la trigonometría, la función inversa de la cosecante es conocida con el nombre de arcosecante de un ángulo. Esta propiedad se simboliza como: arccosec α ó también puede ser identificada como arccsc α. Su significado en geometría es el ángulo cuya cosecante es alfa.

Y = arccsc (x)

X = csc (y)

A partir de esta definición podemos deducir algunas expresiones importantes, tales como:

Arccosec (-x) = – arccosec x

Arccsc (x) = arcsin ( 1 / x )