Seno

La trigonometría es un área que pertenece a las matemáticas la cual es encarga de estudiar todas las diferentes relaciones que pueden llegar a presentarse entre los ángulos y los lados que tiene un triángulo. Para ellos, depende de razones trigonométricas entre las cuales podemos encontrar el seno.

Temas relacionados

Cosecante, coseno, cotangente, teorema del coseno

¿Qué es el seno?

El seno es un tipo de función trigonométrica que está presente en los triángulos rectángulos y que puede ser medido o encontrado cuando se divide el cateto opuesto del triángulo por la hipotenusa del mismo.

Definición

La palabra seno proviene de la palabra latina “sinus” y tiene varios usos, en este caso, lo enfocaremos en el área de las matemáticas. Es una de las seis diferentes funciones trigonométricas que existen las cuales también se conocen con el nombre de funciones circulares. Entonces, en el campo de la trigonometría el seno puede ser definido como la razón que existe entre el cateto opuesto al ángulo y a la hipotenusa.

Existe también un término relacionado con el seno, el cual se conoce como la ley de los senos y ésta establece una relación de proporcionalidad o de relación constante entre las diferentes magnitudes que pueden llegar a ser medidas entre la longitud que tiene cada uno de los lados del triángulo y el seno de cada uno de los ángulos opuestos. También es conocida con el nombre de teorema de senos.

Características del seno

Algunas de las principales características del seno se mencionan a continuación:

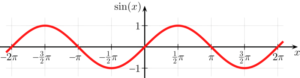
• Su dominio es R.
• Posee un recorrido de [- 1, 1]
• Tiene la capacidad de cortar el eje X en los puntos k·π con k∈Z
• Es impar, en otras palabras, es simétrico con respecto al origen.
• También se caracteriza por ser estrictamente creciente en cuanto a los intervalos de la forma (a, b).
• Es también decreciente.
• Posee infinitos máximos relativos con los puntos de la forma.
• Se encuentra acotada superiormente por el 1 e inferiormente por el -1.

Para qué sirve el seno

El seno puede ser utilizado en varios campos principalmente científico y es considerada como un función de trigonometría bastante importante. Sirve para poder realizar cálculos sobre las distancias que son desconocidas, para medir ángulos y para saber con exactitud las distancias que se han recorrido. En la vida real, es bastante utilizado cuando se necesitan hacer cálculos sobre alturas o también para medir los ángulos de determinados objetos.

Cómo se calcula

La fórmula que se utiliza para poder calcular y encontrar el seno es la siguiente:

Sen B = cateto opuesto / hipotenusa = b / a

Relaciones trigonométricas

En cuanto a las relaciones trigonométricas del seno, éstas pueden relacionarse también con algunas identidades trigonométricas. algunas de ellas son las siguientes:

• El seno es una función impar que se representa como sen (-x) = -sen (x)
• El seno es un tipo de función periódica que funciona con periodo 2 π

Derivada

Para poder averiguar la derivada del seno es necesario utilizar la regla de la cadena la cual es un procedimiento más sencillo que utilizando límites en la derivada de una composición de funciones. Esta regla se representa por medio de la siguiente fórmula:

z’ = sen’ (x² – 2) = 2x cos (x² – 2)

Luego, se deberá de aplicar la fórmula de la derivada:

[sen x]’ = cos x

Integral

La integral del seno se representa de la siguiente manera:

∫ sen x dx = – cos x + C

Dominio y rango

Los dominios de seno son considerados como infinitas, entonces el dominio y el rango del seno son los siguiente:

• Dominio: (-∞, ∞)
• Rango: (-1, 1)

Función inversa del seno

La función inversa del seno se denota de la siguiente manera: y = sin –1 x. Esto puede ser leído como “y es la inversa del seno de x”. Esta frase quiere decir que y es el ángulo que tiene el número real y que su valor de seno es x.

Ejemplos

Algunos ejemplos de seno se mencionan a continuación:

• Seno de 270: -1
• Seno de 90: 1
• De 70: 0.93969
• De 30: 1 / 2
• De 60: √3 / 2
• Seno de pi: 0