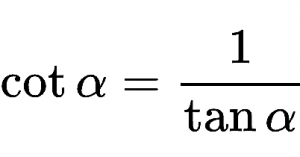Cotangente
La aplicación de funciones trigonométricas en el área de las matemáticas y en otras áreas es ampliamente utilizada en nuestro mundo. Estas funciones son una de las funciones matemáticas básicas en áreas como la triangulación, que se utiliza en investigaciones criminales y servicio celular. También se usan en navegación, topografía, gráficos por computadora y teoría musical. Y una de las áreas más importantes es la función trigonométrica cotangente.
¿Qué es la cotangente?
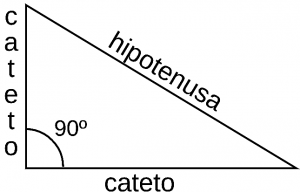
La cotangente equivale al resultado que equivale al cociente entre el cateto adyacente y el cateto opuesto de un arco o de un ángulo. Es la función inversa de la tangente.
Características de la cotangente
Las principales características de la cotangente son las siguientes:
- Es la razón trigonométrica inversa de la tangente.
- Es el recíproco o el inverso multiplicativo de la tangente, es decir tan α · cot α = 1.
- Su abreviatura es cot, cotg o cotan.
- Su dominio es igual a R excepto a · π, siendo a un número entero.
- Tiene un recorrido de la función que es el co-dominio de la cotangente, este es igual a R.
- Su gráfico es una onda cotangentoida.
Para qué sirve
Es utilizada de la misma manera que se usan las funciones seno, coseno y tangente. Puede ser usada en función de un triángulo rectángulo, utilizando los lados opuesto y adyacente del triángulo, o puede usarlo en función del círculo unitario, que muestra los ángulos en radianes.
Si se quiere encontrar la altura que tiene un árbol en particular en función de la sombra que arroja cuando el sol está en un ángulo de 30 grados, podemos encontrar esta información utilizando cotangente utilizando un triángulo 30-60-90.
Sirve también para modelar situaciones reales para los fenómenos físicos que deben de describir ondas como el sonido, el movimiento armónico simple y otros.
Cómo se calcula
Puede ser calculada de la siguiente forma:
Cotangente = Cateto adyacente / Cateto opuesto
En vista de que es la función inversa de la tangente, también puede ser calculada dividiendo 1 por la tangente.
Fórmula
La fórmula para averiguar la cotangente es:
Cot α = 1 / tan α = cateto contiguo / cateto opuesto = b / a
Derivada de la cotangente
La derivada de la cotangente de una función determinada será igual a la derivada de la función con signo negativo dividida por el seno al cuadrado de dicha función:
F (x) = cotg w
F´(x) = ( – w´ ) / ( sen² w )
Aplicando las reglas trigonométricas la derivada de la cotangente también puede ser definida de la siguiente manera:
F´(x) = – w´ · cosec² w
F´(x) = – w´ · ( 1 + cotg² w )
Integral
La fórmula que se utiliza para averiguar la integral cotangente es la siguiente:
∫ csc x sec x dx
Dominio y rango
La tangente y la cotangente se encuentran relacionadas no sólo por el hecho de que son recíprocos, sino también por el comportamiento que presentan sus rangos. En referencia al plano de coordenadas, tangente es y/X, y cotangente es X/y.
Los dominios de estas dos funciones se encuentran restringidas, porque en algunas ocasiones sus relaciones podrían tener ceros en el denominador, pero sus rangos son infinitos.
Para averiguar el dominio de la cotangente deberemos de saber el valor de la misma y luego se procede a dividir:
cos (x) / sen (x)
Es importante mencionar que el sen (x) nunca debe de tomar el valor del número 0.
El dominio de la cotangente comprende el grupo de números reales menos los múltiplos que tenga π para que K sea un entonces un número entero.
¿Cómo citar este artículo?
Briceño V., Gabriela. (2018). Cotangente. Recuperado el 25 febrero, 2024, de Euston96: https://www.euston96.com/cotangente/