Triángulo isósceles

Para iniciar a explicar el triángulo isósceles, debemos recordar también la definición de triángulo. Llamamos triángulo a un polígono que posee tres lados y que está determinado por tres puntos que no son colineales llamados vértices. Debemos también recordar que los vértices se identifican por medio de letras, que son la A, B y C. Un triángulo isósceles es un tipo de triángulo que posee al menos dos de sus lados iguales. Esta propiedad es equivalente a dos ángulos del triángulo que son iguales. Por lo tanto, un triángulo isósceles tiene dos lados iguales y dos ángulos iguales. El nombre deriva del griego iso (same) y skelos (leg).

Temas relacionados

Cateto, hipotenusa, triángulo escaleno, triángulo rectángulo, Pitágoras

¿Qué es el triángulo isósceles?

El triángulo isósceles es un tipo de polígono que está formado por tres lados, esto quiere decir, que está conformado por tres rectas las cuales se cortarán dos a dos y en tres puntos que no se presentan alineados.

Características del triángulo isósceles

Las principales características del triángulo isósceles son las siguientes:

• Eestá formado por tres rectas, éstas rectas se cortarán dos a dos.
• Los puntos en los que las rectas se logran encontrar se conocen con el nombre vértices
• Cada segmento de recta del triángulo isósceles se erige como los lados del triángulo.
• Los dos lados continuos que encontramos en el triángulo isósceles dan origen al ángulo interior.
• El triángulo estará conformado por tres lados como dijimos, por tres vértices, por tres ángulos interiores y por tres ángulos exteriores.

Propiedades

Al igual que otros triángulos, el isósceles tiene sus propiedades, las cuales son:

Los ángulos opuestos a los lados iguales son iguales. La bisectriz del ángulo que se encuentra opuesto a la base, corta a la base en su punto medio. La bisectriz concuerda siempre con la mediana del lado AB. La bisectriz del ángulo opuesto a la base es perpendicular a la base. La bisectriz concuerda con la altura correspondiente que tiene el lado AB.

Como los triángulos isósceles tienen un par de lados iguales, esto les permite que también posean ciertas particularidades bastante reconocidas tanto con respecto a la geometría como en los cálculos de los mismos. Todo triángulo equilátero es también isósceles, pero evidentemente esto no es necesariamente recíproco.

Elementos

En un triángulo isósceles, también existen diferentes elementos que forman parte de él, entre ellas mencionamos las siguientes:

• Bisectriz
• Mediatriz
• Mediana

Altura

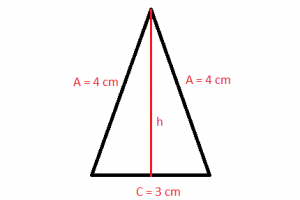
La altura (h) del triángulo isósceles puede ser calculada utilizando el teorema de Pitágoras. Los lados a, b/2 y h forman un triángulo rectángulo. Los lados b/2 y h son los catetos y a la hipotenusa.

h² + (b/2)² = a² → h² + ( b²/4 ) = a² → h² = a² – ( b²/4 )

Obteniendo luego otra fórmula que nos dice que la altura del triángulo isósceles es:

h = √( a² – ( b²/4 ))

Área

El área que tiene un triángulo isósceles puede ser calculada a partir de la base b (el lado no repetido) y la altura (h) del triángulo correspondiente a la base. Podemos decir entonces que, en este caso, el área es el producto de la base y la altura dividido por dos, siendo su fórmula la siguientes:

Área = ( b · √( a² – ( b²/4 )))/2

Perímetro

El perímetro de un triángulo isósceles puede ser obtenido sumando los tres lados que tiene el triángulo. Al tener dos lados iguales, el perímetro es dos veces el lado repetido (a) más el lado desigual de la figura geométrica.

Perimetro = 2 · a + b

Donde a es uno de los lados repetidos y b el otro lado.

Cuanto miden los ángulos de un triángulo isósceles

El triángulo rectángulo isósceles posee un ángulo recto y dos agudos iguales con una medida de 45° cada uno, de esta manera, dos lados del triángulo son iguales y el otro es diferente. A los lados que son iguales se les conoce son los catetos y al ángulo que es diferente se le conoce con el nombre de hipotenusa. Es simétrico respecto a la altura de la hipotenusa, que pasa por el ángulo recto.

Lados congruentes

La congruencia, es el momento en que uno de los lados del triángulo son congruentes, de manera que, dos ángulos podrán ser congruentes si tienen la misma medida y dos trazos son congruentes si tienen la misma longitud. En el triángulo, puede haber correspondencia entre los lados y entre los ángulos. Recordemos que el triángulo isósceles es el tipo de triángulo que tiene dos de sus lados iguales y uno diferente, al tener dos lados con la misma medida, es considerado como congruente.

Calcular los lados de un triángulo isósceles

Los triángulos isósceles tienen dos de sus lados de igual medida y uno de ellos tiene una medida diferente. También se supone que si dos de los lados que tiene un triángulo isósceles son congruentes o iguales, esto quiere decir que los ángulos opuestos a esos lados serán de la misma manera congruentes.

Cuántos ángulos iguales tiene

El triángulo isósceles posee dos de sus ángulos de igual medida, mientras que el tercero siempre será diferente.

Ejemplos

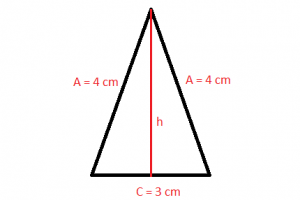
Un ejemplo de triángulos isósceles sería el siguiente: