Isosceles triangle

To begin explaining the isosceles triangle, we must also remember the definition of triangle. We call a triangle a polygon that has three sides and is determined by three points that are not collinear called vertices. We must also remember that vertices are identified through letters, which are A, B and C. An isosceles triangle is a type of triangle that has at least two of its equal sides. This property is equivalent to two angles of the triangle that are equal. Therefore, an isosceles triangle has two equal sides and two equal angles. The name derives from the Greek iso (same) and skelos (leg).

Related topics

Catechus, hypotenuse, scalene triangle, right triangle, Pythagoras

What is the isosceles triangle?

The isosceles triangle is a type of polygon formed by three sides, this means that it is formed by three straight lines which will be cut two by two and in three points that are not aligned.

Characteristics of the isosceles triangle

The main characteristics of the isosceles triangle are as follows:

• It is formed by three straight lines; these straight lines will be cut two by two.
• The points in which the straight lines are found are known as vertices.
• Each line segment of the isosceles triangle is erected as the sides of the triangle.
• The two continuous sides found in the isosceles triangle give rise to the inner angle.
• The triangle will be faced by three sides as we said, by three vertices, by three interior angles and by three exterior angles.

Properties

Like other triangles, the isosceles have their properties, which are:

The angles opposite the equal sides are equal. The bisector of the angle opposite the base cuts the base at its midpoint. The bisector always matches the median on the AB side. The bisector of the opposite angle to the base is perpendicular to the base. The bisector matches the corresponding height of the AB side.

As isosceles triangles have a pair of equal sides, this allows them also to have certain particularities quite recognized both with respect to geometry and in their calculations. Every equilateral triangle is also isosceles, but obviously this is not necessarily reciprocal.

Elements

In an isosceles triangle, there are also different elements that are part of it, among them we mention the following:

• Bisector
• Mediatrix
• Medium

Height

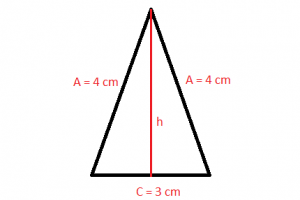
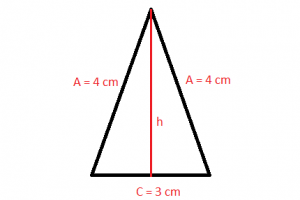
The height (h) of the isosceles triangle can be calculated using the Pythagorean theorem. The sides a, b/2 and h form a right triangle. Sides b/2 and h are the legs and a hypotenuse.

h² + (b/2)² = a² → h² + ( b²/4 ) = a² → h² = a² – ( b²/4 )

Then getting another formula that tells us that the height of the isosceles triangle is:

h = √( a² – ( b²/4 ))

Area

The area that has an isosceles triangle can be calculated from the base b (the unrepeated side) and the height (h) of the triangle corresponding to the base. We can say then that, in this case, the area is the product of the base and the height divided by two, being its formula the following:

Area = ( b · √( a² – ( b²/4 )))/2

Perimeter

The perimeter of an isosceles triangle can be obtained by adding the three sides of the triangle. Having two equal sides, the perimeter is twice the repeated side (a) plus the uneven side of the geometric figure.

Perimeter = 2 · a + b

Where a is one side repeated and b is the other side.

How much do the angles of an isosceles triangle measure?

The isosceles right triangle has a right angle and two acute angles with a measure of 45° each, thus, two sides of the triangle are equal and the other is different. The sides that are equal are known as the cathetus and the angle that is different is known as hypotenuse. It is symmetrical with respect to the height of the hypotenuse, which passes through the right angle.

Congruent sides

Congruence is the moment when one of the sides of the triangle are congruent, so two angles can be congruent if they have the same measure and two strokes are congruent if they have the same length. In the triangle, there can be correspondence between the sides and between the angles. Remember that the isosceles triangle is the type of triangle that has two of its equal sides and a different one, having two sides with the same measure, is considered as congruent.

Calculate the sides of an isosceles triangle

Isosceles triangles have two sides of equal measure and one of them has a different measure. It is also assumed that if two of the sides of an isosceles triangle are congruent or equal, this means that the angles opposite those sides will be congruent in the same way.

How many equal angles it has

The isosceles triangle has two of its angles of equal measure, while the third will always be different.

Examples

An example of isosceles triangles would be as follows: