Right triangle

Triangles are polygons that are formed by three sides, so we can say that the triangle is a flat figure that is formed by three different segments.

Related topics

Cathetus, hypotenuse, Pythagoras, Pythagorean theorem, isosceles triangle, scalene triangle

What is a right triangle?

The right triangle is the triangle that has a right angle which has a measure of 90 degrees and two angles that are acute, which means that they measure less than ninety degrees.

Characteristics of the right triangle

The most important characteristics of right triangles are:

• They are polygons that have three sides.
• They are formed by three segments.
• They all have a right angle of ninety degrees.
• The two angles that are not right will always be acute angles.
• The right angle is made up of the two shorter side
• They can be isosceles or scalene

Properties

Right triangles have several properties that are mentioned below:

• They all have two acute angles and their hypotenuse is larger than the cathetus.
• The square of the hypotenuse is equal to the sum of the square of the cathetus.
• The sum of the hypotenuse and the diameter of a circle inscribed in the triangle is equal to the sum of the cathetus.
• When calculating the area, one cathetus can be considered the base and the other one as the height.
• The median of the hypotenuse breaks down a right-scaled scalene triangle into two triangles.
• The median of the hypotenuse of an isosceles right triangle breaks it down into two congruent and equivalent isosceles right triangles.
• Two right triangles that have a common hypotenuse, and the right angles in opposite half-planes determined by the line containing the hypotenuse, form a birectangular quadrilateral.
• The median that starts from the right angle is equal to half of the hypotenuse.

Right triangle types

There are two different types of right triangles, these are:

• Right isosceles triangle: it is the triangle that has a right angle of 90º and two angles of 45º. The two legs are equal.
• Scalene right triangle: it is the right triangle that has all the different angles always having one of them of 90º. The sides are also different.

Elements

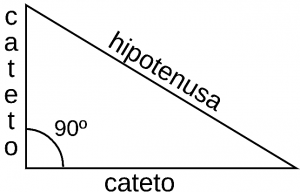
The elements of the right triangle are:

• Cathetus: are the sides of the triangle that together form the right angle.
• Hypotenuse: is the largest side of the triangle opposite the right angle.
• Right angle: is a 90º angle formed by the two legs.
• Acute angles: the other two angles of the triangle (α and β) are less than 90º. The sum of the two acute angles is 90º.

Height

The height of a right triangle can be found using the following theorems:

Height theorem: In any right triangle the height relative to the hypotenuse is the geometric median between the orthogonal projections of the cathetus over the hypotenuse.

h/m = m/h

If we multiply the two equality members by hn then we can get: h2 = mn, so h = √(mn)

Area

The area that has a right triangle will always have a right angle of 90°, so its height must coincide with one of its sides (a). The area of a right triangle is half the product of the two sides that form the right angle (cathetus a and b). The formula for calculating the area of the triangle is as follows:

Area = ( b – a ) / 2

Being b the base and the side that matches the height.

Perimeter

We know as the perimeter of a right triangle the sum of the three sides. To find out we apply a simple formula, which is the following:

Perimeter = a + b + c

Where a, b and c represent the measurements of the triangle.

In addition, the right triangle also complies with the Pythagorean theorem, so the hypotenuse (c) can be expressed from the cathetus (a and b). The formula for this type of operation is as follows:

Perimeter = a + b √(a²+b²)

Where a and b are the cathetus that form the right angle.

Trigonometric ratios

Right triangles have different trigonometric ratios which help us know the relationship between the sides and angles of the triangle. Their main function is to show us how much the internal angles of the triangle measure when we know the lengths of two sides of the triangle. It is important to remember that right triangles always have a 90° angle. There are three common trigonometric reasons that are:

• Sinus: is the reason that exists between the opposite cathetus and the hypotenuse and each of them corresponds to an angle.
• Cosine (cos): is the result of dividing the adjacent side by the hypotenuse.
• Tangent (tan): result of dividing the lengths of the opposite and adjacent sides to the angle α.

Therefore, we have to:

• Opposite Side / Hypotenuse = Angle Sine.
• Adjacent Side / Hypotenuse = Angle Cosine.
• Opposite Side / Adjacent Side = Angle Tangent.

How to calculate the angle of a right triangle

The heights of the right triangles are associated with the cathetus (a and b). Therefore, ha=b and hb=a. The height associated with the hypotenuse is known as hc. The three heights of the triangle converge at the orthocenter, H in the vertex C of the right angle.

In order to calculate the height associated with side c (the hypotenuse), the height theorem is used.

The height h can be obtained by knowing the three sides of the right triangle and the following formula is applied:

H = ( a – b ) / c

The right triangle has a right angle of 90°, so its height matches one of its sides (a). Its area will then be half the product of the two sides that form the right angle (cathetus a and b). The following formula is used:

Area = ( b – a ) / 2

Examples

Some examples of how to solve the areas of right triangles are the following:

Be a right triangle with the sides that form the known right angle (a and b), being a=3 cm and b=4 cm. What is its area?

We apply the previous formula of the area of a right triangle ( b – a ) / 2 and we get that its area is 6 cm².

The area of a right triangle can be obtained from the hypotenuse and the height of the triangle associated with it through the theorem of height.

Let n and m be the projections of the legs (b and a). Then, the area of a right triangle is defined by the following formula:

Area = ( c · √( n·m)) / 2

Formula of the area of a right triangle by the theorem of height. This method is useful if the cathetus  (a and b) are not known.