Ley de Kirchhoff

Dentro del área de la ingeniería eléctrica las leyes de Kirchhoff en conjunto a las de Ohm forman las tres leyes que se consideran básicas en el análisis de los circuito eléctricos y la electrónica, ya que con ellas se pueden comprender los tres elementos o parámetros necesarios dentro de esta área que son la resistencia, el voltaje y la corriente eléctrica.

Temas relacionados

Circuitos eléctricos

¿Qué es la ley de Kirchhoff?

Las leyes de Kirchhoff son dos en las que se fundamenta la conservación de la energía y la carga de circuitos eléctricos, esta fue expuesta por primera vez en el año 1846 por el ingeniero Gustav Kirchhoff y son una de las bases más importantes tanto en el área de la ingeniería eléctrica como en la electrónica. Estas leyes permiten hallar las tensiones y corrientes en cualquier parte de un circuito eléctrico. Este par de leyes de circuitos toman como base la ecuaciones de Maxwell, sin embargo, es Kirchhoff quien precedió a Maxwell y a su vez fue George Ohm quien generalizo estas leyes.

Historia

Fueron creadas en 1845 y se denominaron leyes de Kirchhoff en honor a su creador, quién se basó en la teoría del físico Georg Simon Ohm, se distinguen como una extensión de la ley de la conservación de la energía y son aplicables al cálculo de tensiones, intensidades y resistencias de una malla eléctrica.

Primera ley de Kirchhoff

Dentro de un circuito eléctrico normalmente se generan dos nodos de corriente, se le dice nodo al punto de circuito donde se unen más de una terminal del componente eléctrico, también es llamado nudo, unidos por un punto de soldadura normalmente.

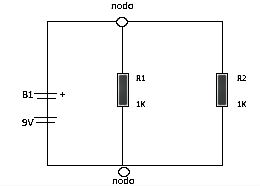
Si se analiza este circuito básico de corriente continua, podemos ver que hay dos resistores de 1khoms cada uno conectado a una misma batería y dos nodos. La batería se encuentra conservando su tensión fija, aunque estén conectados a él los dos resistores; esto da a entender que sobre cada resistor se le encuentra aplicada una tensión de 9 voltios.

Analizando la ley de Ohms nos da a entender que cuando hay una resistencia en este caso uno de 1 kohms y se le aplica una tensión de 9 voltios por el acabara circulando una tensión de 9 mA dándonos a entender que:

1= V/R = 9/1.000 = 0,009 A=9 mA 

Por ende, es seguro que cada resistor va a tomar una corriente 9 mA de la batería o también que entre ambos van a tomar 18 mA de la batería. Se puede decir que de la batería parte un conductor en el que viaja 18mA que al pasar sobre el nodo este se divide, y sigue en diferentes direcciones en este caso hacia R1 y R2, los cuales vendrían siendo cada resistor, llevándole a cada uno 9mA pero cuando vuelven a retornar hacia la batería volverá con el mismo valor de 18 mA debido a que se vuelven a unir como se muestra a continuación.

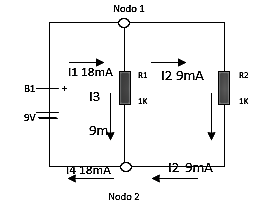
Si aplicamos la lógica determinaremos que en el nodo I es I1=I2+I3

Si colocamos los valores quedaría así:

18mA=9 mA + 9 mA

Y el nodo dos seria la sumatoria siguiente I4= I2 + I3

Por lo que es lógico que I4 es igual I1, esto se debe a que la carga de batería que sale si no se encuentra conectado a algún punto de desgaste esta debe volver con la misma cantidad de la que partió.

El enunciado de la primera ley de Kirchhoff establece que la corriente que pasa por un nodo es igual a las corrientes de la salida; a su vez habla que las corrientes entrantes a un nodo son iguales a la suma de las corrientes salientes.

Segunda ley de Kirchhoff

El enunciado establece que cuando un circuito eléctrico tiene más de una batería y algunos resistores de carga, ya no se ve tan claro como se establecen las corrientes por sí mismo.

Dentro de un circuito cerrado, se determina que la suma de todas las tensiones de las baterías que están dentro del recorrido siempre serán iguales a la sumas de las caídas de la tensión existente en los resistores.

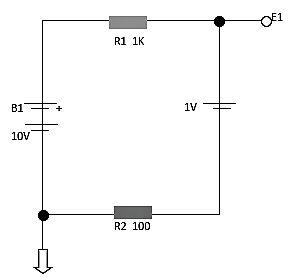
En la figura anterior se ve un circuito que posee dos baterías y dos resistores, lo que se busca determinar es la tensión o el potencial en cada punto con referencia al terminal negativo que se estableció como la tierra.

Las tensiones de fuente son las que se ven escritas en el circuito ejemplo pero si buscamos aplicar la caída de la resistencia en los resistores primero hay que buscar la corriente que circula por él. En la figura las dos fuentes se encuentran conectadas de manera que se encuentren conectadas entre sí por el R1, lo que da a entender que la tensión total no es la suma sino más bien la resta de ambas fuentes.

Estableciendo a la tierra como referencia, la batería asciende su potencial a 10 voltios mientras que la batería B2 baja a 1 voltio, por ende, la corriente que circula en total es 10-1= 9 voltios. Evaluando esto se establece que los electrones que atraviesan de B1 a R1 pero cuando pasa a B2 este pierde potencial y termina atravesando R2. La mejor manera de analizar esto es haciendo un esquema:

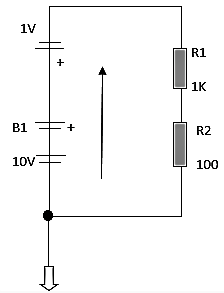
Este circuito no es el original, este se organiza para calcular la corriente original del circuito.

I= Et/R1+R2

Esta fórmula se debe a que los electrones salidos de R1 están obligados a pasar por R2, por ende, es como si el resistor total es la suma de ambos. Se dice que los resistores se encuentran lineales o en serie cuando los vemos como en el esquema anterior que ambos son cargados por la misma corriente.

R1+R2= 1100 ohms

Esto quiere decir que si trasladamos los valores quedaría así:

I = (10-1)/1000 + 100= 0.008170 o 8,17mA

Ahora que conocemos la corriente que circula pero el circuito podemos saber la tensión que es ejercida sobre cada resistor

I = V/R pero si lo despejamos quedaría V =R . I

Y por esto podemos remplazar los valores para saber la caída sobre R2 que sería igual a:

VR2= R2 . I= 100. 8,17 mA = 817 mV

Y en el caso de R1:

VR1= R1 . i= 1000. 8,17 mA = 8,17V

Ya con estos valores de caídas de tensión podemos trasladarnos al cuadro para calcular la tensión deseada:

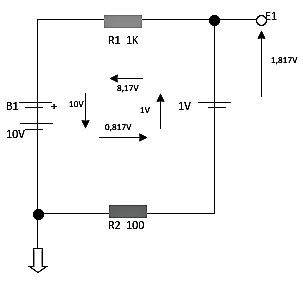
Al ya conocer y lograr ver las cuatros flechas que representan las tensiones de cada fuente, a su vez las caídas de tensión, es ahora cuando podemos ver representada la segunda ley de Kirchhoff, ya que desde el punto de referencia girando en sentido horario podríamos decir que:

10V – 8,17 – 1V – 0,817V = 0

O si se teman los términos dejando que las fuentes estén a la derecha y las caídas de tensión a la izquierda, podríamos decir que las sumas de las tensiones es bastante fuerte:

10V-1V = 8,17 + 8,987 = 9V

Y pudiendo así determinar que la salida de tensión del circuito es de:

8,0817V + 1V = 1,817V

Y como la polaridad se encuentra explicita dentro del circuito de ejemplo podemos decir que esta es positiva.