Velocidad angular

La velocidad angular es menos común que otros tipos de velocidades tales como la velocidad lineal, ya que únicamente puede ser aplicada a objetos que se mueven a lo largo de una trayectoria circular. Por ejemplo, un auto de carreras en una pista circular o una bola de ruleta que gira en una ruleta, todos estos ejemplos tienen una velocidad angular.

• Unidad: rad/s
• Fórmula: ω = dθ/dt

¿Qué es la velocidad angular?

La velocidad angular es una medida de rotación y es la rapidez con la cual puede llegar a variar el ángulo en un transcurso de tiempo y que se puede medir en radianes por segundo.

Definición

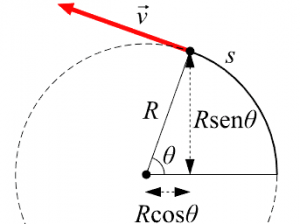
Desde hace miles de años, el área de la física ha buscado la manera de entender la forma en la que se mueven las cosas. Desde este punto de vista, el movimiento se encuentra relacionado con una serie de conceptos diferentes tales como fuerza, velocidad, inercia o gravedad. La velocidad angular de un objeto es el desplazamiento angular que tiene el mismo con respecto al tiempo. Cuando un objeto se desplaza a lo largo de una trayectoria circular, el ángulo central correspondiente a la posición del objeto en el círculo se encuentra en constante cambio. La velocidad angular, representada por la letra ω , es la velocidad de cambio de este ángulo con respecto al tiempo.

Características de la velocidad angular

Las principales características de la velocidad angular son las siguientes:

• Se representa por medio de la letra griega ω.
• Nos indica cuál es el ángulo que recorre un cuerpo en una unidad de tiempo.
• Se representa por medio de un vector perpendicular.
• Cuando la rapidez se da en forma constante deja de existir.

Cómo se calcula la velocidad angular

La velocidad angular en el Sistema Internacional de Unidades se expresa por medio de radianes/segundo (rad/s). El módulo que tiene la velocidad angular de un cuerpo se puede expresar dependiendo del número de vueltas que el cuerpo pueda hacer en la unidad de tiempo, y por esta razón en algunas ocasiones se puede dar por medio de revoluciones por minuto (r.p.m) o por segundo (r.p.s). La velocidad angular puede ser calculada como la variación del ángulo sobre la variación que se da en el tiempo. La velocidad angular puede ser representada de la siguiente forma:

ω = dθ/dt 

Donde:

• ω = representa la velocidad angular [rad/s]
• Δθ = representa la variación que tiene el ángulo [rad]
• Δt = representa el intervalo de tiempo [s]

Tomando en cuenta que la frecuencia es la cantidad de vueltas que se dan sobre el tiempo, la velocidad angular también se puede expresar como:

 ω = 2 π f

Donde:

• ω = representa la velocidad angular [rad/s]
• f = representa la frecuencia [Hz]

Vector de velocidad angular

La velocidad angular es un vector que es perpendicular con respecto al plano de rotación. El vector de velocidad angular o ω, puede ser definido como un vector axial que se encuentra paralelo al eje de rotación y cuyo módulo es el valor de la velocidad angular anteriormente definida, en otras palabras:

ω = dθ/dt

cuya dirección concuerda con el del progreso de un tornillo que gira en el sentido en que lo hace el sólido. Si destinamos por e al vector que indica la dirección del eje, y cuya dirección sea la definida por la regla anterior, tenemos:

ω = dθ/dt e ⇒ ωe = dθ/dt

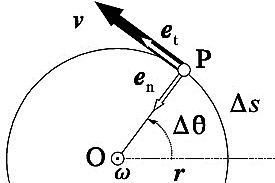
en donde se toma en cuenta el elemento del ángulo dθ como un vector dθ, de módulo dθ, cuya dirección se encuentra definida por la regla del tornillo. Llamando e_t y e_n a los vectores tangencial y normal, respectivamente, a la trayectoria del punto genérico P, la velocidad de ese punto puede expresarse de la siguiente manera:

v = ve_t = r ω ( e_n x e) = (re_n) x (ωe) = PO x ω

por esta razón podemos afirmar que la velocidad v de un punto genérico P de un sólido rígido en rotación será igual al momento del vector velocidad angular ω con respecto a dicho punto P.

Cómo se relaciona con la velocidad lineal

Recordemos que la velocidad angular es el ángulo girado por el móvil en una determinada unidad de tiempo. En otras palabras es la rapidez con la que varía el ángulo a medida que transcurre el tiempo. La velocidad lineal es la longitud del arco recorrido Δs en el tiempo. La velocidad angular es una medida relacionada con la velocidad de rotación y la velocidad tangencial es vista como la velocidad real que tiene un objeto que efectúa el movimiento circular.

Ejemplos

Un ejemplo de cómo calcular la velocidad angular es el siguiente:

Determinar la aceleración angular de un cuerpo que se mueve experimentando un movimiento de rotación, dada expresión de su posición en la rotación Θ (t) = 4 t3 i. (Siendo i el vector unitario en la dirección del eje x). Determine el valor de la aceleración angular cuando han transcurrido 10 segundos del inicio del movimiento.

ω (t) = d Θ / dt = 12 t2i (rad/s)

α (t) = dω / dt = 24 t i (rad/s2)

α (10) = 240 i (rad/s2)